Calculating the Derivative of an Integral Function
Question:
If ![]() , then
, then ![]()
- (A)
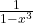
- (B)
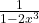
- (C)
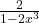
- (D)
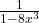
- (E)
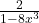
Step-by-Step Solution
- Understand the Function Structure:
Given the function:
![Rendered by QuickLaTeX.com \[ F(x) = \int_{1}^{2x} \frac{1}{1 - t^3} \, dt \]](https://fresherhub.com/wp-content/ql-cache/quicklatex.com-bc7de6d1ce2a38eab6737b4049520ca5_l3.png)
Here, the upper limit of integration is
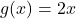 .
. - Apply the Fundamental Theorem of Calculus:
If
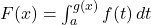 , then:
, then:![Rendered by QuickLaTeX.com \[ F'(x) = f(g(x)) \cdot g'(x) \]](https://fresherhub.com/wp-content/ql-cache/quicklatex.com-c7ee024022db45a0b3ea6b3162be1a55_l3.png)
Where:
- Compute
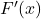 :
:
![Rendered by QuickLaTeX.com \[ F'(x) = \frac{1}{1 - (2x)^3} \cdot 2 = \frac{2}{1 - 8x^3} \]](https://fresherhub.com/wp-content/ql-cache/quicklatex.com-3b146375a15e8c3066df11395941edb2_l3.png)
- Match with the Given Options:
The derivative simplifies to:
![Rendered by QuickLaTeX.com \[ F'(x) = \frac{2}{1 - 8x^3} \]](https://fresherhub.com/wp-content/ql-cache/quicklatex.com-a7aa301a5daff658b13e212fa31b8d11_l3.png)
This corresponds to option (E).
Final Answer
Answer: (E) ![]()
